Record the Past, Map the Future
No matter the time period, our timeline maker simplifies the process of creating timelines. It's adaptable, responsive, and fast to update online, making your timeline creation a breeze.
View your timelines in horizontal or list view. It works on just about any device.
- Add timeline events or multi-date timespans.
- Automatically have your timeline events placed on the appropriate timescale.
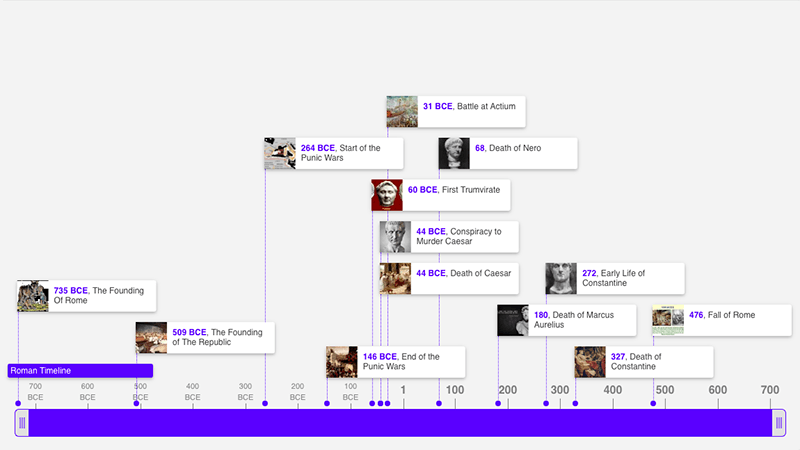
- Zoom and pan your timeline.
- Add historical events with BCE dates, year-only dates, as well as timeline dates with a specific month and day.
- Upload images to bring your timelines to life.
- Adapt to any screen size with our fluid timeline design.